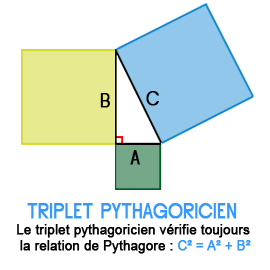
Triplet Pythagoricien

Définition du triplet pythagoricien

Le triplet pythagoricien est un triplet d'entiers naturels non nuls (x; y; z) qui vérifie toujours la relation de Pythagore : x² + y² = z².

Le triplet pythagoricien primitif

Un triplet pythagoricien est primitif si les trois entiers naturels x, y et z sont premiers entre eux.
Exemples : (3, 4, 5) ; (20, 21, 29) ; (11, 60, 61) ; (13, 84, 85) ; (5, 12, 13)

Propriété du triplet pythagoricien

Si (x, y, z) est un triplet pythagoricien primitif, alors x et y sont de parités différentes et z est impair.

Théorème fondamental du triplet pythagoricien

 Il y a équivalence entre :
    - ( x ; y ; z ) est un triplet pythagoricien primitif avec x impair.
    - Il existe m et n entiers non nuls avec m > n , m et n premiers entre eux et de parités différentes       tels que :
I.   x = m² - n²
II.  y = 2mn
III. z = m² + n²